Phase Portrait

A phase portrait is a tool to analyze a dynamic system.

Example

Consider the nonlinear system:

$\begin{align*} \mathbf{f} (\mathbf{x})&= \mathbf{\dot{x}} = \begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \end{bmatrix}\\\dot{x}_1 &= - 2x_1^3 + 10 x_1 - 2 x_2\\ \dot{x}_2 &= 9x_1 - 9x_2 \end{align*}$

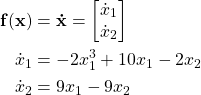
Step 1: Calculate equilibrium points (EPs)

$\begin{align*}\mathbf{\dot{x}} = \mathbf{0}\\\Rightarrow \dot{x}_1 & =-2x_1^3 + 10x_1 - 2x_2=0\\\dot{x}_2 & = 9x_1 - 9x_2=0 \\\\\Rightarrow x_1^* &= x_2^* = \{0, 2, -2\}\\\Rightarrow & \text{EP}_1 = (0,0), \hspace{3mm} \text{EP}_2 = (2,2),\hspace{3mm} \text{EP}_3 = (-2,-2)\end{align*}$

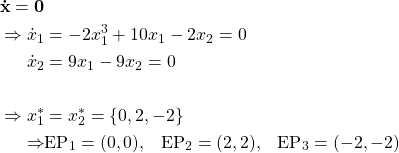
Step 2: Linearization at equilibrium point (Find Jacobi matrix)
Jacobi-Matrix:

$\begin{align*}J &= \begin{bmatrix} \frac{\partial \mathbf{f}}{\partial \mathbf{x}}\end{bmatrix}\\&= \begin{bmatrix} -6 x_1^2 + 10 & -2 \\ 9 & -9\end{bmatrix}\end{align*}$

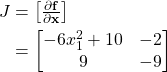
Step 3: Calculate eigenvalues of the Jacobi matrix

$\begin{align*}\text{det}(J - \lambda I) &\overset{!}{=} 0\\&= \text{det}\left(\begin{bmatrix} -6 x_1^2 + 10 - \lambda & -2 \\ 9 & -9-\lambda \end{bmatrix}\right)\\&= (-6x_1^2 +10 - \lambda)(-9-\lambda)+18\\&= -54x_1^2-90+9\lambda +6 x_1^2 \lambda - 10 \lambda +\lambda^2 + 18\end{align*}$

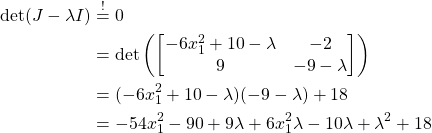
Step 4: Determine characteristics of equilibrium points

Step 5: Calculate eigenvectors

Step6: Sketch

Example

Neueste Beiträge

Neueste Kommentare