General model of dynamic systems, please see Dynamic Systems.
Linearizing at arbitrary Equilibrium Point
Given:
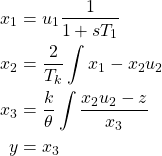
Goal: Find
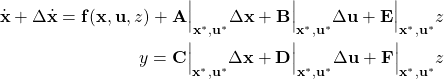
where ![]() is the system matrix,
is the system matrix, ![]() is the input matrix,
is the input matrix, ![]() is the output matrix,
is the output matrix, ![]() is the feedforward matrix, and
is the feedforward matrix, and ![]() and
and ![]() are noise matrices.
are noise matrices.
Step 1: Find state derivatives
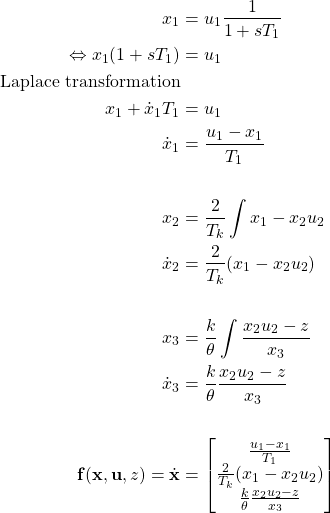
Step 2: Find state equilibrium
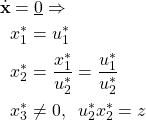
Step 3: Linearization
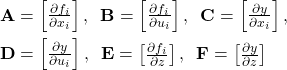
State-space representation:
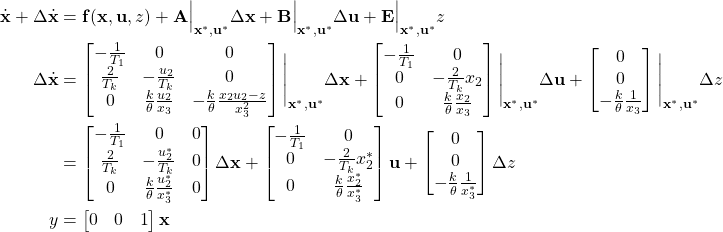
Linearizing along a Reference Trajectory
Given:
![]()
Step 1: Find state space representation
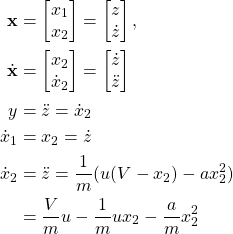

Step 2: Find linearized state space representation
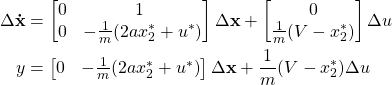
Step 3: Use given reference trajectory to define the optimal state and input
Given: Reference trajectory ![]() , starting from
, starting from ![]() to target
to target ![]() with
with ![]() and
and ![]()
![]()
After inserting ![]() and
and ![]() , we obtain
, we obtain ![]()
Now, we use the state representation:
![]()
We obtain the optimal state:
![]()
Now, we want to find the optimal input of the system
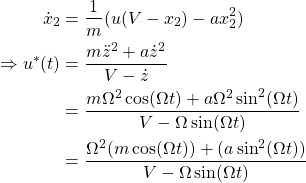
Step 4: Insert optimal values in to the linearized state space representation
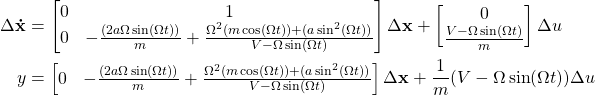

Neueste Kommentare