Structure
- Large-scale system
- Graph indicates coupling
- Nodes are described by „simple“ dynamical subsystems
Goal
Achieve global behavior from local interaction
Problem
Scalability and limited information ![]() Distributed algorithms, local interaction among subsystems
Distributed algorithms, local interaction among subsystems
Rendezvous Problem
Given a team of ![]() robots, how should they move to meet at the same location, using only local information?
robots, how should they move to meet at the same location, using only local information?
Model

How to design 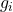 ?
?
Assume: we have two robots ![]() with positions
with positions ![]()
Robot dynamics:
![]()
Rendezvous between
-
 closer to
closer to 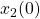
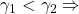 closer to
closer to 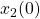
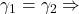 rendezvous in the middle
rendezvous in the middle 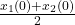
Approach: Rendezvous at host agent 
All agents move to host agent ![]() .
.
Robot dynamic:
![]()
Properties:
- every agent
 has to be able to communicate with the host
has to be able to communicate with the host 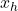
- not robust against host failure
- needs global coordination to elect host
Approach: Rendezvous at midpoint 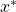
All agents have global knowledge of each agent (e.g. positions, …)
Robot dynamic:
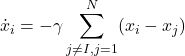
Properties:
- Every agent has to be able to communicate to any other agent
- Not scalable
Approach: Rendezvous reached dependent on set 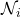
Use local information to find a consensus.
Define a set ![]() of agents sensed by agent
of agents sensed by agent ![]() at time
at time ![]()
Robot dynamic/Consensus:
![]()
Questions:
- For which network/information topology is consensus achieved?
- How to show consensus?
- Where do agents meet?
- Generalisability?

Neueste Kommentare