Regression analysis is an instance of supervised learning. The goal is to estimate the dependent variable ![]() by using the independent variable
by using the independent variable ![]() .
.
Variables
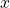 : independent variable, features
: independent variable, features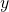 : dependent variable, response
: dependent variable, response : (unknown) noise or error
: (unknown) noise or error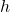 : a function of
: a function of 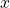
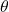 : Parameter or weight vector of the function
: Parameter or weight vector of the function 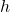
Model
![]()
Goal
Predict the value ![]() corresponding to
corresponding to ![]() that is outside the training set. Find a function
that is outside the training set. Find a function ![]() that fits the dataset
that fits the dataset ![]()
Approach
- We have access to the dataset
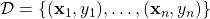 , which is the training set with
, which is the training set with 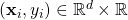 . In theory, we want to find the optimal function
. In theory, we want to find the optimal function 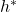 , in practice, we can only estimate the function with the estimate
, in practice, we can only estimate the function with the estimate 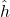 .
. - We assume
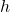 lies under some hypothesis class
lies under some hypothesis class 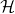 of all available functions.
of all available functions. - We assume that the set of
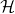 is parameterized with parameter vector
is parameterized with parameter vector 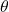 .
. - Example (all functions are linear):
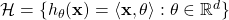
- We now can reduce the optimization problem to the problem of estimating
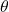
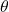 can be learned from the examples or data set
can be learned from the examples or data set 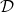
- Find an estimated parameter
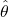 that minimizes the cost function
that minimizes the cost function 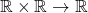
Optimization
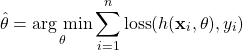
Regression analysis models
- Linear regression
- Ridge regression
- Logistic regression

Neueste Kommentare